Který výraz vystihuje funkci SOUČIN.SKALÁRNÍ nejvýstižněji? Univerzální, všestranná, flexibilní? Je obtížné se rozhodnout, nicméně rozhodne platí, že se jedná o funkci, jejíž uplatnění není omezeno na jeden typ problému. Velice zvláštní na této funkci je, že její popis v nápovědě v podstatě vůbec nenaznačuje praktické využití. Jako by nám tvůrci Excelu záměrně chtěli její možnosti zatajit.
Upřímně řečeno, jaký praktický problém by nám funkce, která vynásobí odpovídající položky uvedených polí (matic) a vrátí součet násobku jednotlivých položek mohla pomoci vyřešit? Po chvíli přemýšlení si možná vzpomeneme, že nám vlastně funkce není zcela neznámá. Na střední škole, v analytické geometrii, nám byla představena a možná jsme ji i několikrát při řešení úloh použili. Nicméně analytickou geometrii 99 % z nás téměř zcela pozapomnělo. Takže k čemu vyvolávat dávno zaprášené znalosti?
Je opravdu velmi překvapující, že tato funkce je vedle funkce INDEX snad nejuniverzálnější funkcí mezi cca 500 vestavěnými funkcemi Excelu. Proč tomu tak je? Zejména právě pro svoji schopnost akceptovat v argumentech matice a oblasti buněk, provést na jejich prvcích matematickou operaci a následně vrátit jedinou hodnotu, což plně vyhovuje konceptu tabulkového procesoru. Tedy konceptu ukládání dat do izolovaných buněk s geometrickým rozložením – principem, kdy oblasti sousedících buněk jsou nositelem logicky souvisejících informací.
Funkce umožňující vyhodnocení jednoduchých podmínek
V základní formě tato funkce vynásobí každý prvek první matice odpovídajícím prvkem v další matici a pak vrátí součet těchto součinů.
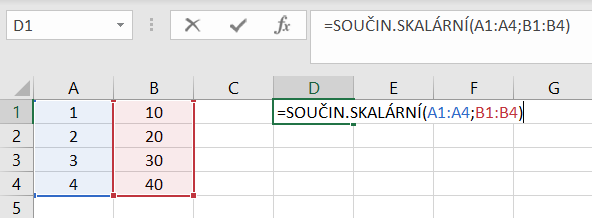
V našem příkladu funkce násobí prvky matice A1:A4 s prvky matice B1:B4 – tedy
1*10 + 2*20 + 3*30 + 4*40 = 10+40+90+160 = 300
Na základě tohoto příkladu tedy vidíme, že tato funkce je užitečná, ale vlastně k čemu? Dobrá zpráva je, že bylo objeveno (záměrně používám toto slovo) mnoho příkladů, v nichž použití této funkce umožnuje efektivní a logické řešení problému. Objevování témat a postupů, ve kterých je využití funkce užitečné, však rozhodně není ani zdaleka ukončeno – doslova každým dnem se na diskuzních serverech objevují nové problémy a jejich řešení pomocí této funkce.
Funkce pro řešení podmíněných výpočtů
Excel obsahuje dvě mimořádně užitečné funkce, které umožnují řešit úlohy podmíněných výpočtů – zejména určení poctu prvku a součtu hodnot. Těmito funkcemi jsou COUNTIF a SUMIF, případně jejich rozšířené verze COUNTIFS a SUMIFS. Umožňují řešit reálné problémy vyhodnocením násobných podmínek (například určení prodeje v termínu OD – DO, určení průměrného platu pracovníků ve věku OD – DO apod.).
Samozřejmě lze násobné podmínky vyhodnotit také pomocí maticových vzorců.
=SUMA(KDYŽ(testA;KDYŽ(testB,….)
avšak toto řešení má minimálně dvě nevýhody:
· Není příliš přehledné
· Je provázeno obecným neduhem maticových vzorců – zpomalením výkonu a rychlosti odezvy
Omezení funkce SOUČIN.SKALÁRNÍ (které lze ale obejít)
Bohužel však pro parametry funkce SOUČIN.SKALÁRNÍ platí následující pravidlo:
Položky pole, které nejsou číselného typu, zpracovává funkce SOUČIN.SKALÁRNÍ jako nuly.
Znamená to tedy, že vzhledem k výše uvedenému pravidlu je výsledkem součinu pravdivostních hodnot vždy hodnota 0, a to dokonce i tehdy, když násobíme dvojici PRAVDA * PRAVDA. Řešení omezení platného pro vstupní argumenty funkce je založeno na transformaci pravdivostních hodnot na číselné hodnoty – konkrétně pravdivostní hodnotu PRAVDA nahradíme číselnou hodnotou 1 a pravdivostní hodnotu NEPRAVDA nahradíme hodnotou 0.
Způsoby transformace pravdivostních hodnot
Je zřejmé, že funkce SOUČIN.SKALÁRNÍ bude vzhledem ke svému použití v oblasti vyhodnocování výběrových podmínek vždy obsahovat pravdivostní hodnoty jako výsledek tohoto vyhodnocování.
Je tedy nezbytné naučit se ovládat techniky, které nám umožní pravdivostní hodnoty převést na hodnoty číselné a tím změnit vstupní argumenty na tvar, který je funkcí akceptovatelný. Dobrou zprávou je, že v současné době uživatelé a vývojáři Excelu již objevili a popsali 6 základních postupů, které nám pomohou potřebný převod hodnot uskutečnit.
Jedná se o následující techniky:
- použití operátoru hvězdička ( * ) mezi jednotlivými argumenty
- vynásobení argumentu hodnotou 1
- přičtení hodnoty 0 k argumentu
- umocnění argumentu jedničkou (^1)
- použití dvojice unárních operátoru ( – – ) před argumentem
- použití funkce N() na argument
- a samozřejmě i kombinace těchto metod v rámci funkce SOUČIN.SKALÁRNÍ
Použití operátoru hvězdička
Nejčastější způsob zápisu vzorců s využitím funkce SOUČIN.SKALÁRNÍ je založen na ověření hodnot odpovídajících výběrovým kritériím. Výrazy sloužící k tomuto ověření jsou navzájem kombinovány pomocí operátoru hvězdička ( * ).
=SOUČIN.SKALÁRNÍ((matice1=kritérium1)*(matice2=kritérium2)*(matice3))
Není to však jediný možný způsob zápisu vzorce. Stejný výsledek získáme i pomocí vzorce v následující struktuře
=SOUČIN.SKALÁRNÍ((matice1=kritérium1)*(matice2=kritérium2);(matice3))
Tento druhý typ zápisu vzorce je založen na důsledné aplikaci pravidla, které nám říká, že operátor hvězdička (*) je určen pro transformaci matic obsahujících logické hodnoty PRAVDA / NEPRAVDA na číselné hodnoty 1 a 0. Pokud však matice obsahuje numerické hodnoty, je použití operátoru hvězdička nadbytečné. Přesněji řečeno, použití tohoto operátoru vede v těchto případech ke zpomalení zpracování vzorce, protože při jeho vyhodnocení Excel využívá nadbytečnou proceduru. Tyto dva přístupy k vyhodnocení komplexních podmínek povedou v naší úloze určení celkového součtu prodeje telefonu Nokia v lednu k zápisu
a)
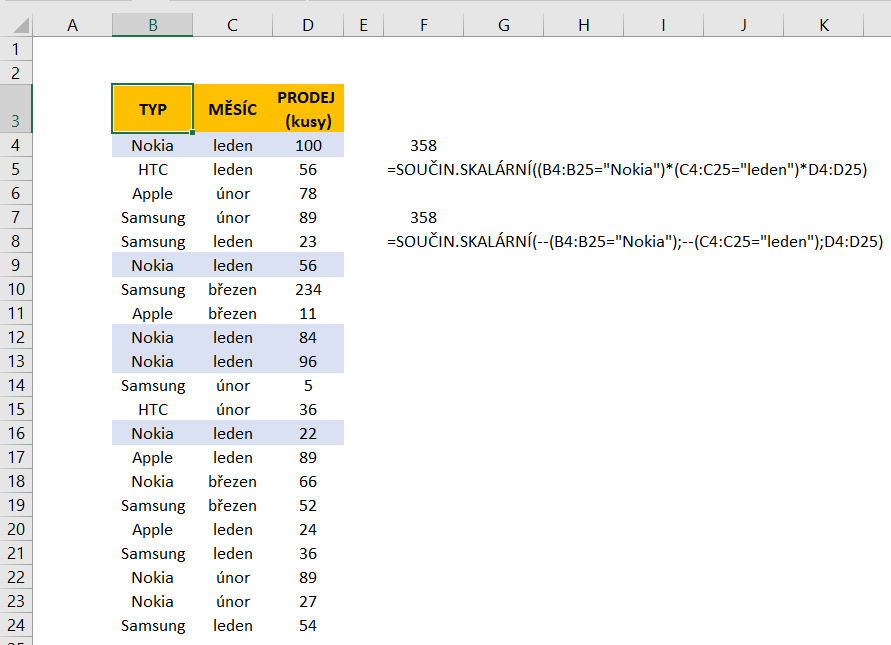
=SOUČIN.SKALÁRNÍ((B4:B25=“Nokia“)*(C4:C25=“leden“)*D4:D25)
b)
=SOUČIN.SKALÁRNÍ(–(B4:B25=“Nokia“);–(C4:C25=“leden“);D4:D25)
Další možnosti transformace logických hodnot
Použití operátoru hvězdička není jediný způsob, umožňující matice obsahující logické hodnoty převést na matice s hodnotami numerickými.
Dalšími variantami jsou:
· vynásobení argumentu hodnotou 1
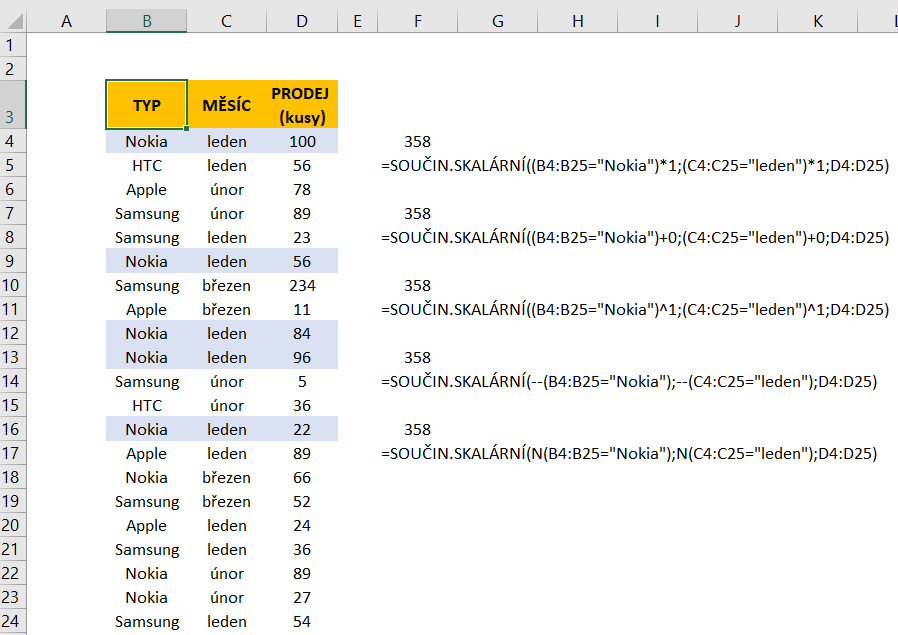
=SOUČIN.SKALÁRNÍ((B4:B25=“Nokia“)*1;(C4:C25=“leden“)*1;D4:D25)
· přičtení hodnoty 0 k argumentu
=SOUČIN.SKALÁRNÍ((B4:B25=“Nokia“)+0;(C4:C25=“leden“)+0;D4:D25)
· umocnění argumentu jedničkou (^1)
=SOUČIN.SKALÁRNÍ((B4:B25=“Nokia“)^1;(C4:C25=“leden“)^1;D4:D25)
· použití dvojice unárních operátorů (- -) před argumentem (operátor mění znaménko operandu, pokud jej použijeme opakovaně, je zachována původní hodnota – v našem případě logických hodnot jsou však tyto hodnoty převedeny na čísla 0 a 1)
=SOUČIN.SKALÁRNÍ(–(B4:B25=“Nokia“);–(C4:C25=“leden“);D4:D25)
Stejný výsledek dostaneme pochopitelně i v případě, že operátor aplikujeme na argument, který obsahuje numerické hodnoty. Tento postup je však nadbytečný, hodnota argumentu se nezmění.
=SOUČIN.SKALÁRNÍ(–(B4:B25=“Nokia“);–(C4:C25=“leden“);–(D4:D25))
Operátor (-) lze však v případě sudého poctu výběrových kritérií použít i bez nutnosti duplikace. Je tomu tak proto, že použitím tohoto operátoru změníme logickou hodnotu NEPRAVDA na číslo (0) a logickou hodnotu PRAVDA na číslo (-1) . Pokud je výběrových kritérií sudý počet, pak v rámci funkce SOUČIN.SKALÁRNÍ při vynásobení argumentu je vždy výsledkem kombinace nepravdivých podmínek číslo 0, kombinace pravdivých podmínek nám vrátí hodnotu (+1) a kombinace pravdivých a nepravdivých podmínek poskytne opět hodnotu 0.
Lze tedy říci, že roli druhého operátoru (-) přebírá sama funkce SOUČIN.SKALÁRNÍ. Je třeba však znovu zdůraznit, že tento postup musíme volit velice uvážlivě, protože nezbytným předpokladem je existence sudého počtu kritérií.
· použití funkce N – tato funkce převádí hodnotu zadanou ve vstupním argumentu na číslo. Z hlediska našich potřeb je důležité, že logickou hodnotu PRAVDA převádí na číslo 1, logickou hodnotu NEPRAVDA na číslo 0.
=SOUČIN.SKALÁRNÍ(N(B4:B25=“Nokia“);N(C4:C25=“leden“);D4:D25)
Kombinace jednotlivých postupů
Výše uvedené postupy lze v rámci jednoho vzorce kombinovat. Například můžeme argument odpovídající jednomu kritériu převést na číselnou hodnotu násobením jedničkou, další argument transformujeme pomocí funkce N.
=SOUČIN.SKALÁRNÍ(N(B4:B25=“Nokia“);(C4:C25=“leden“)*1;D4:D25)
=SOUČIN.SKALÁRNÍ((B4:B25=“Nokia“)+0;(C4:C25=“leden“)*D4:D25)
=SOUČIN.SKALÁRNÍ(–(B4:B25=“Nokia“);N(C4:C25=“leden“);D4:D25)
=SOUČIN.SKALÁRNÍ(1*(B4:B25=“Nokia“);0+(C4:C25=“leden“);D4:D25)
Který z výše uvedených postupů doporučit? Odpověď není snadná ani jednoznačná. Pokud budeme sledovat konference věnované problematice excelovských funkcí, zjistíme, že se jedná o věc osobního přesvědčení a snad i vkusu. Nicméně lze říci, že použití funkce N() může obecně vést k prodloužení doby výpočtu, protože Excel volá vestavenou funkci. Ostatní metody však v žádném případě nelze „sestavit“ podle výkonnostních kritérií, protože každá z nich se může osvědčit u některé specifické úlohy a zároveň u jiného typu úlohy může pracovat nejpomaleji.
Osobně dávám přednost použití dvojice unárních operátorů (- – ) a na druhé místo bych dosadil násobení dvojice argumentu pomocí operátoru hvězdička ( * ). Druhé místo s ohledem na fakt, že tato metoda je nepoužitelná v případě, kdy testujeme pouze jedno kritérium. Metoda založená na dvojici unárních operátoru je však použitelná vždy.
Jeden z největších znalců Excelu, ekonom Harlan Grove, zdůvodnil v jedné konferenci svoji preferenci metody dvojice unárních operátoru následujícími slovy:
„ … jak jsem již poznamenal, nejde při použití dvojice unárních operátorů jen o rychlost výpočtu, která se mi samozřejmě líbí, ale i o skutečnost, že tento zápis není tak náchylný ke vzniku chyb z přepsání, jako je tomu u variant ^1, *1, +0. Protože jsem zvyklý číst zleva doprava, dávám přednost transformaci a úpravám dat v tomto směru, což plně odpovídá použití ( – – ). Nadto mi tento způsob zápisu připadá méně rušivý než použití ostatních variant. Zapouzdření logických výrazů funkcí N() je z hlediska stylu dalším „čistým“ postupem, ale vyžaduje volání funkce, a proto tento postup nepoužívám.“


